Since the previous post, I have added three more functionalities:
First, as delineated last time, I suspect the jiggling motion of the flock simulation I showed last time was due to the individual members making too large turns between time steps. Animals all have a maximum degree they can turn with respect to their orientations (imagine a vector draw from its body to its head). It is more natural to define turning directions in terms of polar coordinates (angles) rather than Cartesians. What I have done is to keep a register of the direction each member is moving at (the angle theta and phi are defined with respect to the positive x-axis). One can quite easily transform between polar and Cartesian.
The code is as below, appended into the flock class. Here, each member are still moving randomly, but only within a restricted angle (45 degree by default).
def directionalVel(self):
self.updateCollisions()
#TODO world dimension
speed = np.random.normal((self.world.dim[0][1] - self.world.dim[0][0])/float(self.world.resolution), 0.001, self.members)
theta = np.add(np.random.normal(0, self.orientation/2, self.members) , [i[0] for i in self.directions] )
if len(self.world.dim) == 3:
phi = np.add(np.random.normal(0, self.orientation/2, self.members) , [i[1] for i in self.directions] )
x = np.multiply(speed, np.multiply(np.sin(phi), np.cos(theta)))
y = np.multiply(speed, np.multiply(np.sin(phi), np.sin(theta)))
z = np.multiply(speed, np.cos(phi))
coords = [ x, y, z ]
self.updateDirections(np.transpose([theta, phi]))
return self.updatePositions(np.transpose(coords))
x = np.multiply(speed, np.cos(theta))
y = np.multiply(speed, np.sin(theta))
coords = [x, y]
self.updateDirections([[i] for i in theta])
return self.updatePositions(np.transpose(coords))
The part that restricts the change in direction between time steps is going to be important when it comes to actually simulating swarms.
Secondly, I have added the detection for any collisions between flock members. As you probably have seen, the depth perception from the simulation visualisation is not very good, there is no way to determine whether two members are overlapping from purely looking. To do this, the pair-wise distance between members need to be calculated.
The pair-wise distance of the flock members is as below, using spatial class in the scipy package. The positions of every member in the flock is stored in the self.positions numpy array. Here, the euclidean distance between pairs makes the most sense for me. This is also in the flock class.
def updateCollisions(self, oriColor = 'green', colColor = 'red'):
# default color collision to red
collisions = self.isCollision()
#self.colors[collisions] = colColor
#self.colors[~collisions] = oriColor
self.colors = [colColor if i in collisions else oriColor for i in xrange(self.members) ]
def isCollision(self, lim = 0.01):
# Condesned matrix format
disMat = spatial.distance.squareform(self.pairDistance() < lim)
return [int(i[0]) for i,v in np.ndenumerate(np.sum(disMat, axis = 0)) if v > 1] # only overlap with itself
def pairDistance(self):
return spatial.distance.pdist(self.positions)
Combing the first two modifications yields the following simulation video:
At the start few second of the video, you can see some of the points are red, indicating members are overlapping. I hope you observe that the jittering motion seen in the last post has disappeared here.
Lastly, to make the analysis somewhat more quantitative, I have written a plotting function to show how the distance between the members in a flock evolve with time. This is a simple function defined in the world class. Where time step is plotted on the x-axis and the sum of all pair-wise distance at a time step is plotted on the y.
def plotAvgDist(self, flock, func, iter = 1000):
x = []
y = []
for i in xrange(iter):
x.append(i)
y.append(np.sum(flock.pairDistance()))
flock.positions = func()
plt.plot(x,y)
plt.show()
This is how the total pair-wise distance evolve with time for the animation above (in 1000 time step):
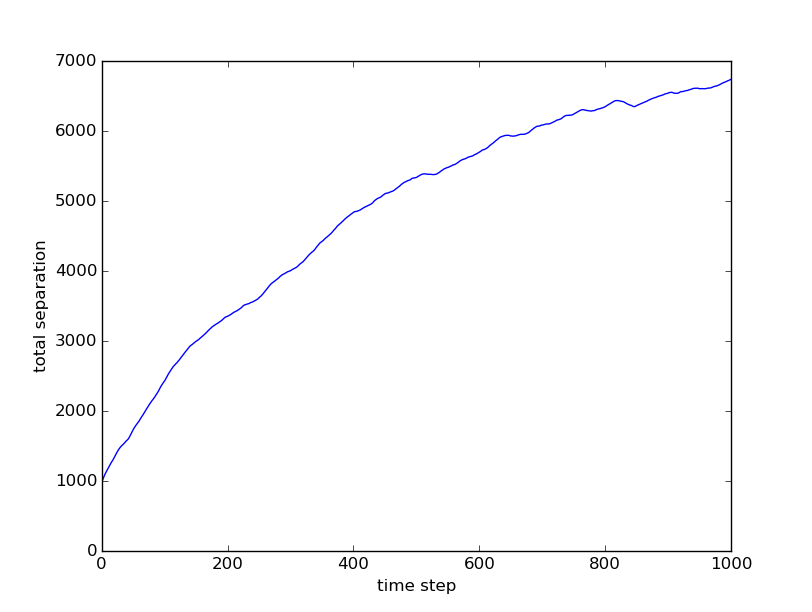
For something exhibiting flock behaviour, I would expect the plot not be a incrementing function. Instead, there ought to be oscillation around a certain value as the transient behaviour.
For the full code, visit my GitHub page for this project : https://GitHub.com/hjuinj/Flock-Simulation
With these, I think I have the necessary framework at hand which allows me to write simple functions to mimic different motions, with the aim to achieve flock behaviour. One immediate idea to mind is having each member of the flock flying towards its closest neighbour, given the posed change in direction constraint. But that’s for the next time…